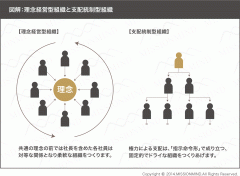
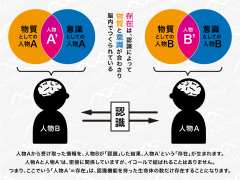
素数の秘密
数学の世界において、素数ほど奇妙な存在はない。規則があるようでなく、無秩序のようでいて完全な無秩序でもない。数直線上にまばらに現れ、かと思えば突然密集する。予測できそうで、決してできない。その曖昧さは、むしろ宇宙の構造それ自体に似ている。
素数とは何なのか。「1と自分自身でしか割れない数」という説明を聞いても、その本質はつかめない。しかし、素数の立ち現れ方をよく見ると、そこには数学を超えた何かが潜んでいる。
素数はしばしば「無駄」に見える。複合数のように他の数を構成する部品でもない。周期を持たず、法則にも従わない。だが、この無駄こそが大きな役割を担っている。
宇宙には、膨大な銀河と星々がある。その大半は、私たちにとって意味があるようには見えない。だが、無数の試行錯誤の「余白」がなければ、生命が育つ条件は生まれなかった。効率とは無縁だが、結果を生むために必要だった無駄である。
素数もこれと同じ構造を持つ。数の世界の中で、素数は「無駄の連続」に見えるが、その散らばりがあるからこそ数学の体系は安定し、複雑さを獲得する。暗号理論、情報工学、波の解析、物理法則の基礎構造。いずれも素数の存在なしには成立しない。
では、なぜ素数だけがこのような特異なふるまいをするのか。
それは、素数が「完全性が破れた瞬間の痕跡」を数の上に残しているからである。数学の体系は本質的に連続した秩序を持つが、その中には必ず「ひび割れ」のような地点が現れる。そのひびこそ素数であり、そこから新しい秩序が生まれていく。
言い換えれば、素数とは「差異が生まれる地点」である。どれほど整数が続いても、素数だけはその流れを断ち切る。連続性の中に突然生まれる「飛び石」のような存在だ。そこでは、数の空気がガラリと変わる。
さらに興味深いのは、素数には「孤立しているのに基盤を支えている」という逆説的な性質があることだ。数学のすべての複合数は素数の組み合わせでできている。つまり、素数は孤立しているが、すべての構造の母体でもある。
この逆説性は、自然界にも広く見られる。秩序は、必ず不連続点によって支えられる。音楽は休符があるからリズムになる。言葉は沈黙によって意味を持つ。自然界の模様も、連続ではなく「切れ目」があるから美しくなる。
素数も同じだ。数の世界に生まれた切れ目を一つ一つたどると、そこから新しい構造が立ち上がる。この「切れ目の存在」こそが、あらゆる創発の起点になる。
素数が暗号に使われるのは、その孤立性ゆえだ。素数が周期をもたず、他の数に依存しない自由点であるため、誰にも予測できず、誰にも分解し尽くせない。そこに揺らぎと強靭さが同居している。
つまり素数とは、「秩序が生まれるための、もっとも原初的なゆらぎ」である。
数の世界は論理で作られるが、その基盤には論理を超えた「感性的な配置」が潜んでいる。素数は、まさにその配置の痕跡だと言える。
無駄であり、遊びであり、予測不能。だがその無駄がなければ、世界の秩序は立ち上がらない。
素数とは、宇宙が残した最古の「遊びのリズム」である。
